Activity 16: Support Vector Machines

🕑07:14, 21 Nov 2019

For this activity [1, 2], I used the extracted fruit color features in space from a previous activity. I used only the data for oranges and apples, and assigned them labels of & , respectively. The objective for SVM is

which is a quadratic and hence, convex problem. Here, is the reference vector perpendicular to the decision line, is the feature vector, is the output classification, and is the bias. Using the Python CVXPY library [3], we can setup the above objective and constraint as-is and directly obtain . Since we have two features, the separating hyperplane is a line defined by

so we can plot the margins on opposite sides of the decision line using trigonometric identities:

Figure 1 shows the optimum decision boundary with maximized margins in the feature space, along with the input data points and support vectors.

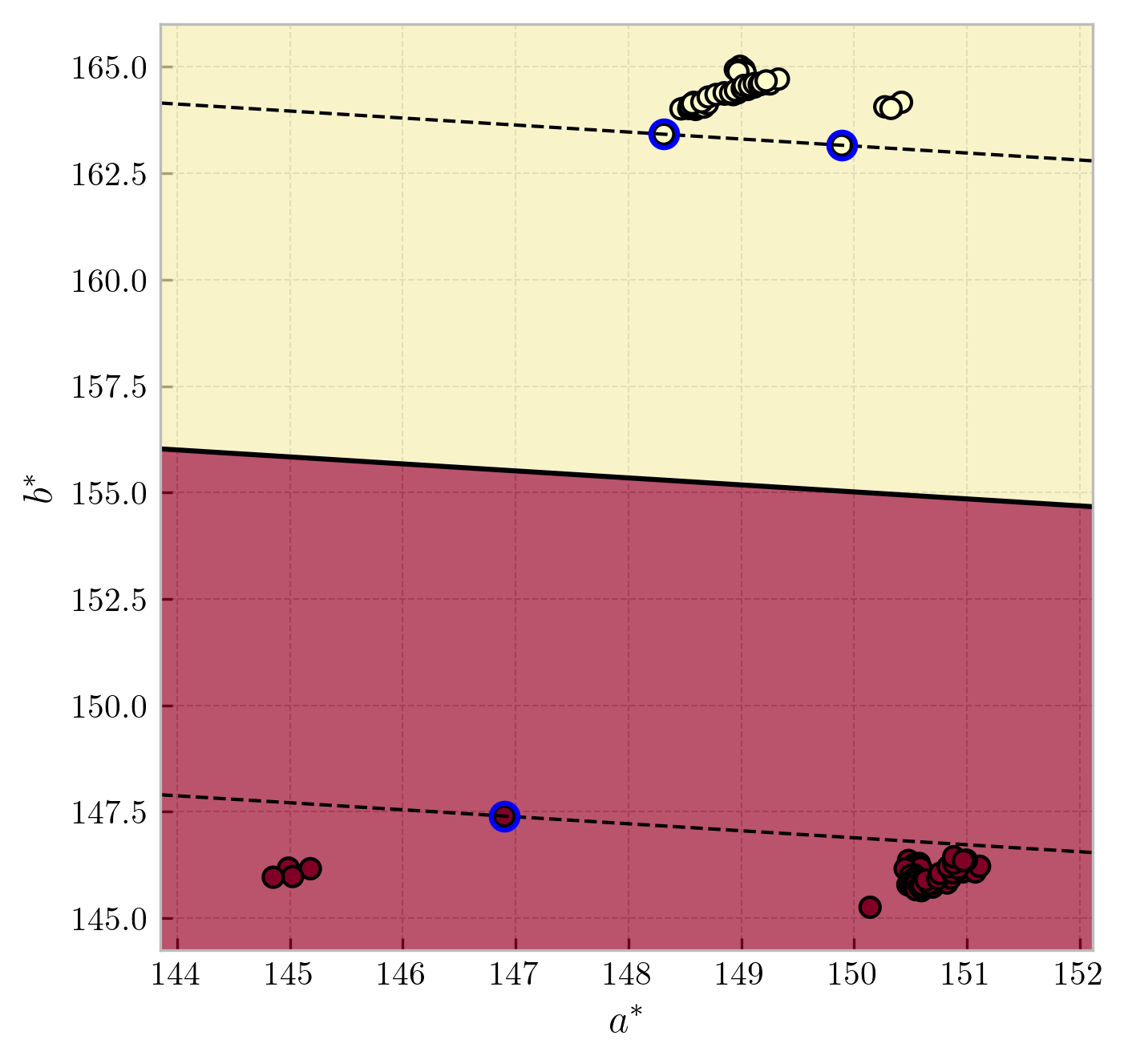
SVM decision boundary

Figure 1: Decision boundary for oranges and apples data in feature space. The yellow region corresponds to a classification of -1 (oranges), while the red region corresponds to +1 (apples). The vectors highlighted in blue are the support vectors. The solid line is the decision boundary, while the dashed lines are the margins.

References

  1. M. N. Soriano, A16 - Support vector machines (2019).
  2. O. Veksler, CS434a/541a: Pattern recognition - lecture 11 (n.d.).

  3. S. Diamond, and S. Boyd, CVXPY: A Python-embedded modeling language for convex optimization, Journal of Machine Learning Research 17(83), 1-5 (2016).

Keywords

image processing
computer vision
support vector machines
feature extraction
object classification